Analysis of trajectories II
In the previous chapter it was shown that the motion of a Navicula on a smooth substrate can be described by the trajectory of a point P to which the apical axis of the diatom is tangential. In addition a more or less strong “wagging” occurs around the direction of movement.
As mentioned at the outset, it is striking that in this example the path, which the leading apex describes, looks smoother than the outer path of the trailing apex. The following drawing shows that this is an immediate consequence of the position of P:
The closer the point P is to an apex the smoother its trajectory and the bumpier the trajectory of the opposite apex. If one follows the path of diatoms visually, one can often see with some experience which end shows the larger fluctuations and conclude on which side of the diatom the center of rotation P is located.
From the magnitude of the fluctuations the position of P can be determined in different ways. As the drawing shows, the amplitudes of the fluctuations relate as the distances of the apices to P. I didn't try to calculate P from the ratio of fluctuations of the movements of the apices, because I expected inaccurate results.
A more suitable alternative criterion for determining P is the magnitude of the fluctuations. As P is the point of rotation of the directional fluctuations, there should be no fluctuations in the case of uniform motion. Due to the fact that the velocity of the diatoms can change rapidly, it is convenient to consider only transverse fluctuations (perpendicular to the trajectory of P). It is therefore possible to use as a criterion that no or only slight transverse fluctuations should occur at the point P. In the following diagram the variance of the transverse fluctuations against the hypothetical values for P is plotted. This was obtained by comparing the observed motion to the smoothed curve (low-pass filtering):
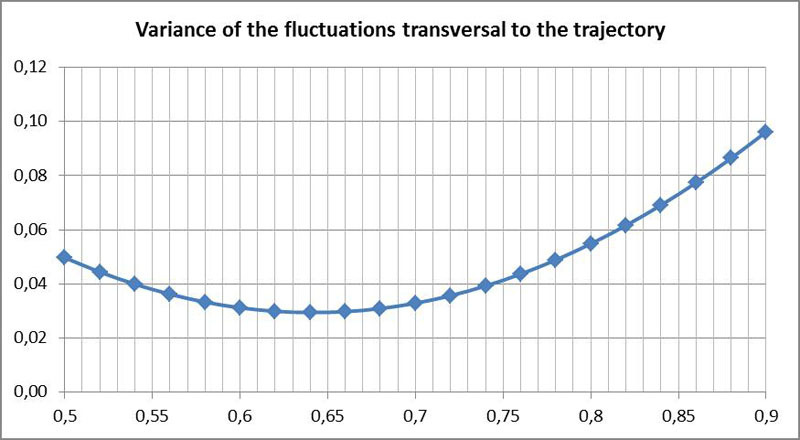
Here, a somewhat smaller value is obtained. That means P is closer to the center. This is probably due to a lower accuracy of the method.
At this point an important remark is to be made. The definition of P using the requirement that the apical axis is tangent to the trajectory of P is fulfilled for straight paths for each point on the apical axis. It does not provide a criterion for the determination of P. However, a determination by consideration of the fluctuations remains usable. Basically a different definition of P is used here. Thereby, P is defined as the pivot point for the fluctuations, i.e., the deviations from a perfect tangential movement. The very restrictive conditions on the form of the raphe in the practical use of the earlier described tangent method do not occur. This method should therefore be preferred.
It turns out that some large diatoms have only a very small fluctuation around the direction of motion. If they move in a straight line, there is no specific point P. P is not needed to describe the trajectories of the apices, as their trajectories are identical and a pair of coordinates is sufficient to describe the path.
If the diatom moves only a short distance between two reversal points, this can prevent a determination of P. Here, an observation from a horizontal view helps.
Interpretation
Navicula and many other diatoms have no valve, which has a larger planar surface in the valvar plane. Such diatoms do not lie horizontally on a flat substrate. In case of Navicula there is a vaulted valve between the apices. Therefore, only a short section of the raphe is in contact with the substrate at a time. The point P lies in this contact area and represents the center of force of the drive.
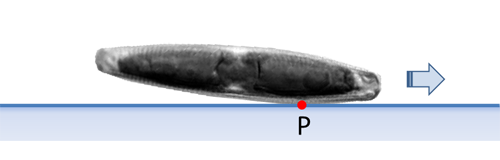As already mentioned, this is proven by images which are made perpendicular to the apical plane (side view), while the diatom with the raphe touches the substrate and moves. The inclination angle of the axis of the apical axis to the substrate, and thus also the position of P, will typically be reached after a certain time from the last reversal point and fluctuate to a certain extent during the movement. The behavior in the vicinity of the reversal points and the observation in side view will be discussed elsewhere.
For all four observed species of Navicula, the point P was on the side of the leading apex. Accordingly, this apex was closer to the substrate and one can say that the diatom is pulled. In case of other diatoms the point P is closer to the trailing apex so that they are pushed. An example is the movement of Craticula cuspidata. Here, the position of P values was around 0.2.
In the general opinion the curvature of the trajectory is produced by the curvature of the raphe (Round et al., 2007). This sounds plausible, at least, for the diatoms, which rest at a short section of the valve. It is only necessary to consider the curvature of the raphe at point P. If the radius of the path is large compared to the length of the diatom, this means an almost inconspicuous curvature of the raphe. Images of Navicula show that there is a curvature in the correct order of magnitude at P. Even a raphe which is straight at first sight often has a sufficient curvature for macroscopic circular paths. I think it is also conceivable that spatial irregularities in extruded EPS influence the path. Even in the case of Craticula cuspidata one can occasionally observe curved paths.
The curvature of the raphe at the point P is presumably not always solely responsible for the size of the paths’ radii. If the valve rests flat on the substrate, the raphe system contributes to the locomotion as a whole. In addition, the friction force of the valve on the substrate must not be neglected. P can then no longer be interpreted as the center of force.
An example of this is an observed species of Pinnularia. One recognizes that the diatom is drawn, the force coming from a region near the leading apex. The trajectories are not everywhere smooth, but an evaluable fluctuation around the direction of movement did not occur (see picture on the left). As Pinnularia has a fairly flat valve, the diatom rests level and a simple mechanical interpretation of P as the center of the driving force is not meaningful. Also the influence of the friction is probably essential. In addition, Pinnularia is often surrounded by a thick layer of mucilage, whose role is not clear with respect to motility. The Raphe has a complicated structure. It is almost closed over a long distance. I assume that for the movement of Pinnularia the tongue-shaped end of the raphe, the so-called helictoglossa, is of particular importance. It could be essential to the position of P near the apex.
For the clearly visible circular paths that e.g. Nitzschia, Cymatopleura and Rhopalodia species exhibit, friction could play an important role. When the raphe is in contact with the substrate, it is not positioned in the center. The friction forces and driving forces act at different points of the valve and could contribute to the formation of the circular paths.
It should not be concealed that the model presented is suitable above all when certain conditions prevail. Only in the case of well-trackable, sufficiently long and smooth trajectories a meaningful analysis is possible. It was pointed out that a simple interpretation of the observations requires a small contact area on the raphe. Some species show irregular patterns of motion that cannot be covered by these methods. One example is the Cymatopleura elliptica (see video on the page about creating cultures and care).
F. E. Round; R. M. Crawford; D. G. Mann (2007), Diatoms: Biology and Morphology of the Genera, Cambridge University Press; 1 edition (2007)