Analyse der Trajektorien I
Auf der vorhergehenden Seite wurde die Verfolgung einer Trajektorie einer Navicula mit Hilfe des Video Spot Trackers gezeigt. Das Ergebnis als Screendump ist oben links zu sehen. Importiert man die Koordinaten in eine Excel-Datei, so kann man dies als Diagramm darstellen, wie es rechts oben dargestellt ist (zum Vergrößern anklicken). Da der Video Spot Tracker den Koordinatenursprung in die linke obere Ecke des Videos legt und die positiven Achsen nach rechts und unten zeigen, sind die Bahnen gespiegelt dargestellt.
Die Trajektorie besteht aus einer längeren spiralförmigen Kurve. Laut Round et. al. (2007) bewegen sich Navicula auf einer geraden Bahn, da ihre Raphe nicht gekrümmt sei. Bei mir haben sie das nie getan. Diese Eigenschaften der Trajektorie halte ich weiterhin für bemerkenswert:
- Der vorauseilende Apex beschreibt eine Kurve, die näher am Krümmungsmittelpunkt liegt als die Bahn des nacheilenden Apex.
- Die Bahnen sind nicht völlig glatt, wobei die innere Bahn geringere Schwankungen aufweist. Zwar führt auch ein nicht gut sitzender Tracker zu statistisch schwankenden Ortskoordinaten, aber diese aufgezeichneten Schwankungen beschreiben überwiegend die Bewegung der Zelle.
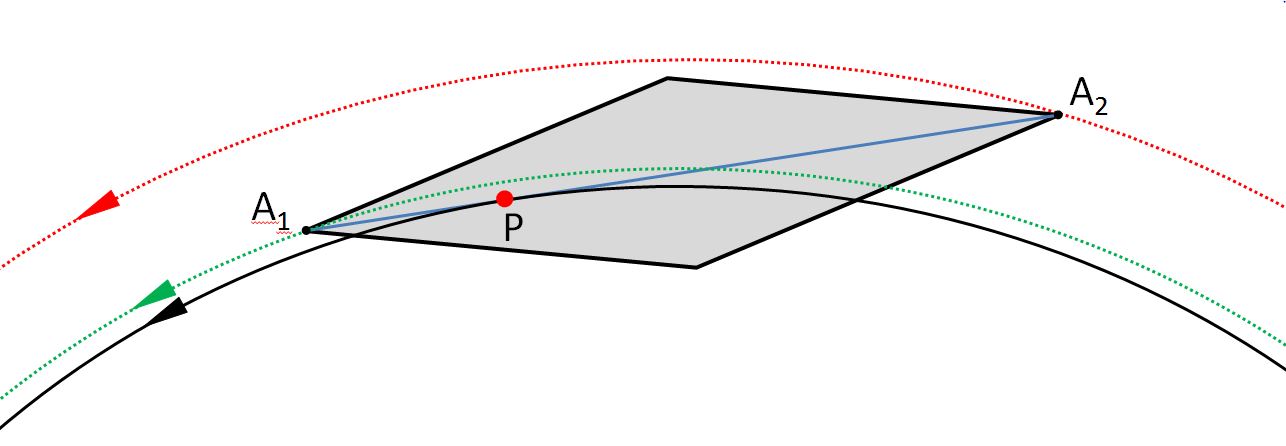
Bei Diatomeen wie Navicula befindet sich das Raphensystem in einem schmalen Bereich um die Verbindungslinie zwischen den Apizes. Bis auf das distale Ende besitzt die Raphe eine so geringe Krümmung, dass Tangenten an die Raphe in guter Näherung parallel zur Verbindungslinie durch die Apizes liegen. Eine Hypothese für die unterschiedlichen Bahnen der Apizes ist, dass es einen Punkt P auf der Raphe gibt, so dass die Diatomee (genauer gesagt ihre Apikalachse) in einer guten Näherung tangential an der Bewegungsbahn dieses Punktes P liegt. Die nachfolgende Zeichnung zeigt diese Annahme:
Die beobachteten Bahnen sind rot und grün punktiert dargestellt. Wenn die Hypothese zutrifft, kann man sich bei der Beschreibung der Bahn der Diatomee (bis auf Fluktuationen) auf die schwarze Bahn beschränken, welche der Punkt P durchläuft. Die Verwendung eines Koordinatenpaares genügt dann.
Wenn man aus einem kurzen Bahnabschnitt die beiden lokalen Bahnradien der beobachteten Kurven ermittelt, lässt sich mit elementarer Geometrie der Abstand von P zu A₁ berechnen. Angesichts der Ungenauigkeit der Bestimmung der Radien an einem kurzen Kurvenstück und der stochastischen Störung hat sich dieser einfache Ansatz nicht bewährt.
Weit genauer ist Bestimmung von P, wenn man eine Annahme zu seiner Position trifft und dann entlang der ganzen zur Verfügung stehenden Trajektorie den Winkel zwischen der Tangente an die Trajektorie des hypothetischen P und der Apikalachse bewertet. Dazu eignet sich sehr gut die Summe der Quadrate der Winkel zwischen Tangentenvektor und Apikalachse. Das gesuchte P minimiert die mittlere quadratische Abweichung (Varianz) dieser Winkel. Durch Variation der Lage des angenommenen Punktes findet man schnell das Minimum.
Es zeigt sich übrigens, dass man als Kriterium ebenso die aufsummierten Skalarprodukte zwischen Tangentenvektor und Apikalachse verwenden kann.
Als hinderlich erweisen sich die teils recht starken stochastischen Überlagerungen. Deshalb wurde die Kurve tangential und transversal durch ein FIR-Filter (Tiefpass) geglättet.
Mittels simulierter, künstlich gestörter Bahnen kann man prüfen, ob das Verfahren valide Resultate liefert. Es hat sich dabei gezeigt, dass die Analyse zuverlässige Resultate erbringt.
Zur hier vorgestellten speziellen Bahnkurve zeigt der folgende Graph die Varianz der Winkel aufgetragen gegen die Position des angenommenen Punktes P:
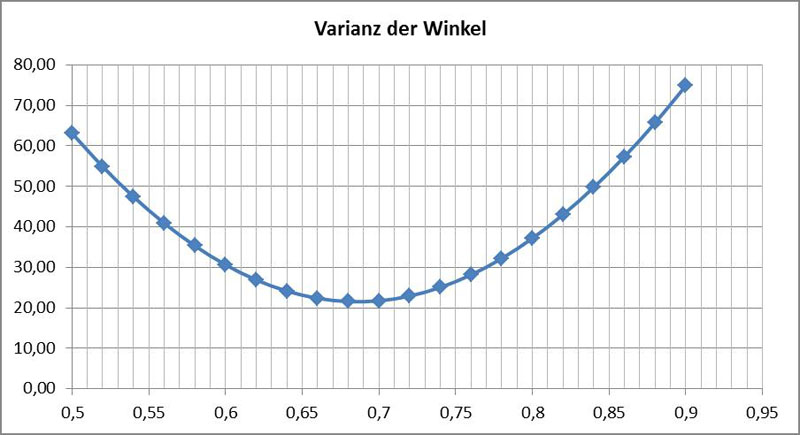
Dabei werden als Referenz für die Lage des Punktes P die Positionen der Tracker verwendet. Der Wert 0 entspricht hier dem nachlaufenden Tracker, der Wert 1 dem voreilenden Tracker. Bei 0,5 liegt der Punkt genau zwischen den Trackern. Da die Tracker nicht exakt an den Apizes sitzen, sondern etwas nach innen gerückt, muss eine Korrektur durchgeführt werden. Auf der normierten Strecke A₁A₂ liegt das Minimum bei 0,64. Der Punkt P liegt auf der Seite des Apex in Bewegungsrichtung, wie dies auch in der obigen Skizze exemplarisch gezeigt ist. Als Trajektorie der Diatomee bezeichne ich nur die Bahn des Punktes P.
Die Analyse anderer Trajektorien derselben Spezies brachte häufig ähnliche Werte. Die Werte bei 10 Analysen lagen zwischen 0,58 und 0,77. Zwei andere Spezies von Navicula lieferten etwas geringere Werte.
Da die Ausrichtung der Diatomee um die Richtung der Tangente an die Trajektorie von P schwankt, lässt sich die Häufigkeit der Winkelabweichung in einem Histogramm darstellen:
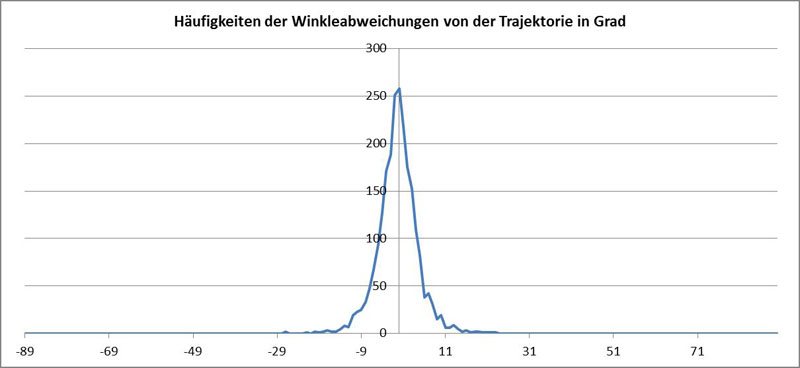
Hierbei wurde der gemessene Wert für P verwendet. Bei inkorrekter Lage von P ist diese Häufigkeitsverteilung nicht symmetrisch zum Ursprung.
Die Existenz des Punktes P mit dem beschriebenen Zusammenhang zwischen Tangente an die Trajektorie und Ausrichtung der Apikalachse ist heuristischer Natur und sollte kritisch gesehen werden. Andererseits hat sie sich bei den untersuchten Navicula spec. gut bewährt.
Bei der nachfolgenden Auswertung sieht man Verteilung der Geschwindigkeit (gemessen in µm/Sekunde):
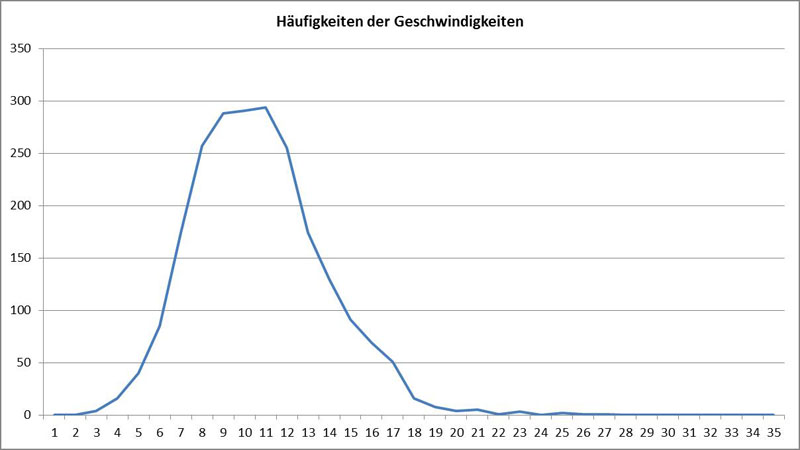
Der Mittelwert lag bei 10,16 µm/s und die Standardabweichung bei 3,07 µm/s. Es erleichtert die Vorstellung, wenn man die Geschwindigkeiten der Diatomeen auf ihre Größe bezieht, sie also in der Maßeinheit „Körperlänge pro Sekunde“ angibt. In diesem Fall liegt dieser Wert bei 0,25 Längen pro Sekunde. Die Geschwindigkeit kann selbst bei einer Spezies sehr unterschiedlich sein. Bei Navicula reicht die beobachtete Spanne von wenigen µm/s bis nahezu 20 µm/s. Es zeigt sich, dass diese Werte stark von Umwelteinflüssen wie der Lichtfeldstärke abhängen. Manche Arten werden erst bei Tageslicht mobil, andere bewegen sich auch in der Nacht.