Analyse der Trajektorien II
Im vorhergehenden Beitrag wurde gezeigt, dass die Bewegung einer Navicula auf glattem Substrat sich durch die Trajektorie eines Punktes P beschreiben lässt, zu der die Apikalachse der Diatomee tangential liegt. Zusätzlich tritt ein „Schwänzeln“ um die Bewegungsrichtung auf.
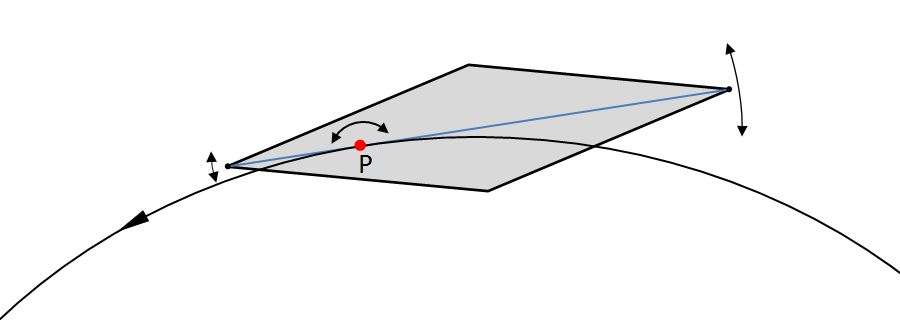
Wie eingangs erwähnt, ist es auffallend, dass in diesem Beispiel die Bahn, die der voreilende Apex beschreibt, glatter aussieht als die äußere Bahn des nacheilenden Apex. Die folgende Zeichnung verdeutlicht, dass dies eine unmittelbare Folge der Position von P ist:
Je näher der Punkt P an einen Apex liegt, desto glatter wird dessen Trajektorie und desto unruhiger die Trajektorie des entgegengesetzten Apex. Wenn man die Bahn von Diatomeen visuell verfolgt, kann man mit ein wenig Erfahrung häufig erkennen, welches Ende die größeren Schwankungen ausführt und daraus schließen, auf welcher Seite der Diatomee der Drehpunkt P liegt.
Aus der Größe der Fluktuationen lässt sich auf unterschiedliche Weise die Lage von P bestimmen. Wie die Zeichnung zeigt, besitzen die Amplituden der Fluktuationen dasselbe Verhältnis wie die Abstände der Apizes zu P. Eine Berechnung von P aus dem Verhältnis der Fluktuationen der Bewegungen der Apices habe ich nicht versucht, da ich ungenaue Resultate erwarte.
Ein besser geeignetes alternatives Kriterium zur Bestimmung von P ist die Größe der Fluktuationen. Da P der Drehpunkt der Richtungsfluktuationen ist, sollte es bei gleichförmiger Bewegung dort keine Fluktuationen geben. Da sich die Geschwindigkeit der Diatomee jedoch schnell ändern kann, ist es zweckmäßig, nur transversale Fluktuationen (senkrecht zur Trajektorie von P) zu betrachten. Man kann also als Kriterium verwenden, dass am Punkt P keine oder nur geringe transversale Fluktuationen auftreten sollten. Im nachfolgenden Diagramm ist die Varianz der transversalen Schwankungen gegen die hypothetischen Werte für P aufgetragen. Diese wurde durch Vergleich der beobachteten Bewegung zur geglätteten Kurve (Tiefpassfilterung) gewonnen:
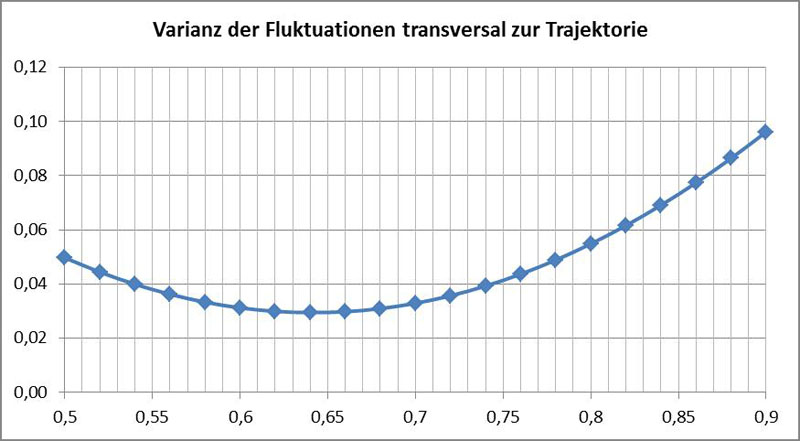
Es ergibt sich hier ein etwas kleinerer Wert, d.h. P liegt zentraler. Vermutlich ist dies auf eine geringere Genauigkeit des Verfahrens zurückzuführen.
An dieser Stelle ist eine wichtige Anmerkung zu machen. Die Definition von P über die Forderung des Tangierens der Apikalachse an die Trajektorie von P ist bei geraden Bahnen für jeden Punkt auf der Apikalkachse erfüllt. Sie liefert dann kein Kriterium für die Ermittlung von P. Eine Bestimmung durch Betrachtung der Fluktuationen bleibt aber nutzbar. Letztlich liegt hier eine andere Definition von P zugrunde. Dabei ist P als Drehpunkt für die Fluktuationen definiert, also über die Abweichungen von einer perfekten tangentialen Bewegung. Die sehr einschränkenden Bedingungen an die Form der Raphe bei der praktischen Nutzung des vorher beschriebenen Tangenten-Verfahrens treten nicht auf. Deshalb ist dieser Methode der Vorzug zu geben.
Es zeigt sich, dass manche großen Diatomeen nur eine sehr geringe Fluktuation der Bewegungsrichtung besitzen. Wenn sie sich in gerader Linie bewegen, gibt es keinen ausgezeichneten Punkt P. P wird zur Beschreibung der Trajektorien der Apizes nicht benötigt, da ihre Trajektorien identisch sind und ein Koordinatenpaar zur Beschreibung der Bahn genügt.
Legt die Diatomee zwischen zwei Umkehrpunkten nur kurze Strecken zurück, so kann das eine Bestimmung von P mit den beschriebenen Verfahren verhindern. Hier hilft eine Beobachtung aus horizontaler Blickrichtung.
Interpretation
Navicula und viele andere Diatomeen besitzen keine Valve, die in der Valvarebene eine größere ebene Fläche besitzt. Solche Diatomeen liegen auf einem ebenen Substrat nicht horizontal auf. Statt dessen weist Navicula eine zwischen den Apizes gewölbte Valve auf. Deshalb hat nur ein kurzer Abschnitt der Raphe zu einem Zeitpunkt Kontakt mit dem Substrat. Der Punkt P liegt in diesem Kontaktbereich und repräsentiert gewissermaßen das Kraftzentrum des Antriebs.
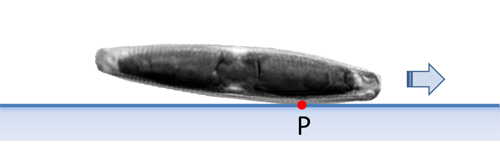Wie bereits erwähnt, belegen dies Aufnahmen, die senkrecht auf die Apikalebene (Seitenansicht) gemacht werden, während die Diatomee mit der Raphe das Substrat berührt und sich bewegt. Der Neigungswinkel der Apikalachse zum Substrat und damit auch die Lage von P stellen sich typisch erst nach einer gewissen Zeit vom letzten Umkehrpunkt ein und schwanken auch bei längerer Bewegung in einem gewissen Umfang. Auf das Verhalten im Bereich der Umkehrpunkte und die Beobachtung in Seitenansicht gehe ich an anderer Stelle ein.
Bei allen vier beobachteten Spezies von Navicula lag der Punkt P auf der Seite des vorauseilenden Apex. Dementsprechend befand sich dieser Apex näher am Substrat und man kann sagen, dass die Diatomee gezogen wird. Bei anderen Diatomeen liegt der Punkt P näher am nachlaufenden Apex, so dass sie geschoben werden. Ein Beispiel ist die Bewegung von Craticula cuspidata. Hier ergaben sich für die Lage von P Werte um 0,2.
Nach allgemeiner Ansicht wird die Krümmung der Trajektorie durch die Krümmung der Raphe erzeugt (Round et. al. (2007)). Dies klingt zumindest für die Diatomeen plausibel, die nur ein einem kurzen Stück der Valve aufliegen. Man muss dann lediglich die Krümmung der Raphe im Punkt P betrachten. Wenn der Radius der Bahn groß gegenüber der Länge der Diatomee ist, bedeutet das eine fast unauffällige Krümmung der Raphe. Bilder von Navicula belegen, dass es eine Krümmung in der korrekten Größenordnung bei P gibt. Auch eine auf den ersten Blick gerade Raphe weist oft eine ausreichende Krümmung für makroskopische Kreisbahnen auf. Ich halte es auch für denkbar, dass räumliche Ungleichmäßigkeiten der EPS-Absonderung die Bahn beeinflussen. Selbst bei Craticula cuspidata kann man gelegentlich gebogene Bahnen beobachten.
Die Krümmung der Raphe am Punkt P ist vermutlich nicht immer allein verantwortlich für die Größe der Bahnradien. Ruht die Valve flach auf dem Substrat, tragen die Raphensysteme insgesamt zum Vortrieb bei. Zudem darf man nicht die Reibungskraft der Valve am Substrat vernachlässigen. P kann dann nicht mehr als Zentrum der Kraft interpretiert werden.
Ein Beispiel dafür ist eine beobachtete Art von Pinnularia. Man erkennt, dass die Diatomee gezogen wird, wobei die Kraft aus einem Bereich nahe dem führenden Apex kommt. Die Bahnen sind nicht immer gleichförmig, doch ein auswertbares Pendeln um die Bewegungsrichtung trat nicht auf (siehe Bild links). Da die Pinnularia eine recht ebene Valve aufweist, liegt die Diatomee flächig auf und eine einfache mechanische Interpretation von P als Zentrum der Antriebskraft ist nicht sinnvoll. Auch der Einfluss der Reibung ist vermutlich wesentlich. Dazu kommt, dass Diatomeen der Gattung Pinnularia oft von einer dicken Schleimschicht aus Polysacchariden umgeben sind, deren Rolle bei der Bewegung nicht ersichtlich ist. Die Raphe weist einen komplizierten Bau auf. Sie ist über eine weite Strecke nahezu geschlossen. Ich vermute, dass für die Bewegung von Pinnularia das zungenförmige Ende der Raphe, die sogenannte Helictoglossa, von besonderer Bedeutung ist. Sie könnte wesentlich für die Lage von P nahe dem Apex sein.
Bei den deutlichen Kreisbahnen, welche Nitzschia-Arten, Cymatopleura und Rhopalodia besitzen, könnte die Reibung eine besondere Rolle spielen. Bei Kontakt der Raphe zum Substrat liegt diese nicht zentrisch. Die Reibungskräfte und Antriebskräfte greifen an unterschiedlichen Stellen der Valve an und könnten zur Bildung der Kreisbahnen beitragen.
Es soll nicht verschwiegen werden, dass sich das hier vorgestellte Modell vor allem eignet, wenn bestimmte Bedingungen herrschen. Nur bei gut verfolgbaren, ausreichend langen und glatten Trajektorien gelingt eine aussagekräftige Analyse. Es wurde darauf hingewiesen, dass eine einfache Interpretation der Beobachtungen eine kleine Berührungsfläche auf der Raphe erfordert. Einige Spezies zeigen irreguläre Bewegungsmuster, die sich diesen Verfahren entziehen. Ein Beispiel ist Cymatopleura elliptica (Video auf der Seite zum Anlegen und Pflege von Diatomeen-Kulturen).
F. E. Round; R. M. Crawford; D. G. Mann (2007), Diatoms: Biology and Morphology of the Genera, Cambridge University Press; 1 edition (2007)