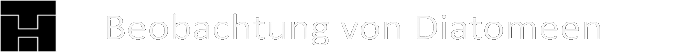Größenfolge der Diatomeen in einer kettenförmigen Kolonie III
Ein überraschender Zusammenhang zwischen Größenfolge und Drachenkurve
Auf der vorhergehenden Seite wurde dargestellt, dass man die Folge der Differenzen der Längenindizes benachbarter Diatomeen bei einer kettenförmigen Kolonie nach einem einfachen Schema berechnen kann. Für die praktische Beobachtbarkeit dieser Folge muss Synchronizität der Teilungen vorausgesetzt werden. Hier soll eine graphische Interpretation dieser Folge vorgestellt werden. Nähere Details sind in der Veröffentlichung (3) zu finden.
Zur Erinnerung: Geht man davon aus, dass die Entwicklung der Größenfolgen mit dem Axiom L0 begonnen wird, so ergeben sich die Folgen der Größenindizes aus dem beschriebenen L-System zu (siehe auch (4)):
g0 = 0
g1 = 0 1
g2 = 0 1 2 1
g3 = 0 1 2 1 2 3 2 1
g4 = 0 1 2 1 2 3 2 1 2 3 4 3 2 3 2 1
….
Die zugehörigen Differenzfolgen sind:
d1 = 1
d2 = 1 1 -1
d3 = 1 1 -1 1 1 -1 -1
d4 = 1 1 -1 1 1 -1 -1 1 1 1 -1 -1 1 -1 -1
….
Würde man statt mit dem Größenindex 0 mit j >0 starten, so würde jeder Index der Größenfolge um den Wert j zu erhöhen sein. Die Folgen der Differenzen bleiben unverändert. In (3) wird gezeigt, dass man auch für die Folgen der Differenzen ein Lindenmayer-System (L-System) angeben kann.
Bei L-Systemen werden die entstehenden Folgen oft durch eine Turtle-Graphik (auch Igelgrafik genannt) visualisiert. Dabei wird die erzeugte Folge (z.B.) von links nach rechts durchlaufen, wobei abhängig vom Buchstaben in der Folge ein bestimmter Befehl ausgeführt wird. So kann man abhängig vom Buchstaben eine Drehung um einen Winkel ausführen, den Stift heben oder senken, die Farbe ändern etc. Es sollen diese Regeln verwendet werden:
- Gehe um eine Längeneinheit vorwärts.
- Stoppe die Bewegung, falls das Ende der Folge erreicht ist.
Ansonsten: Lese den nächsten Buchstaben, danach Rechtswendung um 90° beim Wert 1, Linkswendung um 90° beim Wert -1. - Gehe zu 1. (Sprungbefehl)
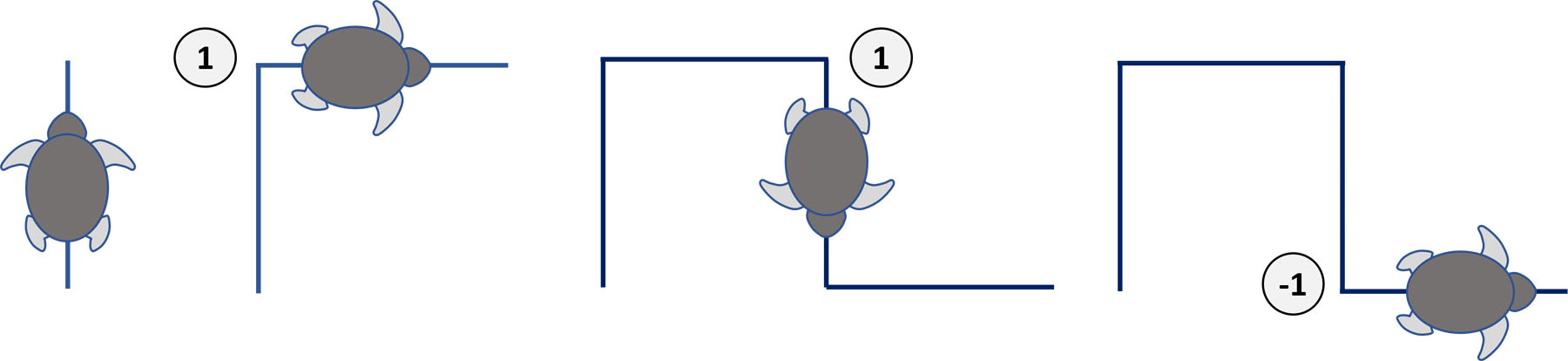
| Mit d4 = 1 1 -1 1 1 -1 -1 1 1 1 -1 -1 1 -1 -1 ergibt sich dieses Bild: | Dieses Video zeigt die Entstehung der 6. Generation: |
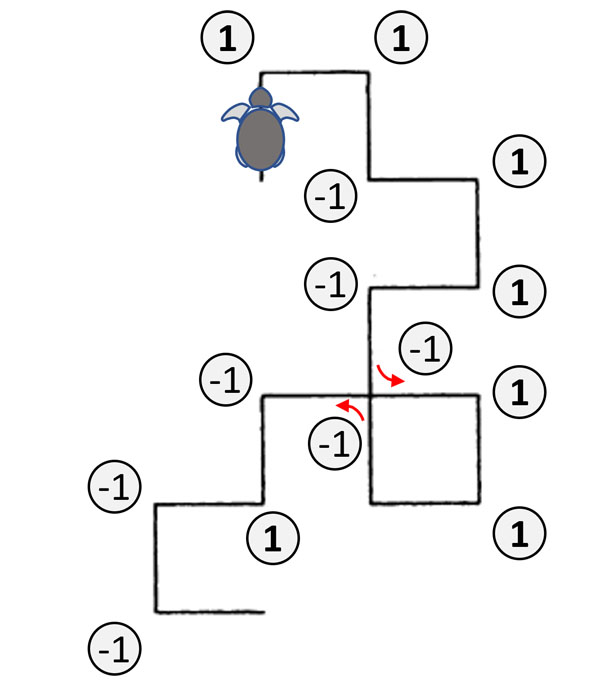 |
Diese Folgen und deren Visualisierung sind bekannt. Die Kurven werden als (Heighway-) Drachenkurven bezeichnet (Wikipedia). Drachenkurven treten in den Diatomeen-Ketten in dem Sinne auf, in dem das Pascalsche Dreieck auftritt, nicht als geometrische Figur, sondern als mathematische Struktur.
Drachenkurve der 13. Generation. Sie enthält 213 - 1 = 8192 Winkel.
Entspricht ein Fragment einer Diatomeen-Kolonie der theoretischen Folge, so kann man einen Teil einer Drachenkurve erzeugen, indem man Diatomee für Diatomee auf Längenunterschiede prüft und eine Turtle-Grafik in der beschriebenen Weise erzeugt. Ist die betrachtete Diatomee größer als die vorhergehende, so führt man eine Rechtsdrehung (Differenz = 1) aus, ist sie kleiner, so führt man eine Linksdrehung (Differenz = -1) aus. Ein Beispiel einer korrekten Abfolge bei einer Eunotia-Kette mit 25 Diatomeen ist in (3) zu finden.
Die Eigenschaften der Drachenkurven sind gut untersucht. Aussagen über sie können unmittelbar auf die Diatomeen-Kolonien angewendet werden. Drachenkurven sind exakt selbstähnliche Fraktale. Sie ist im Grenzfall n→∞ flächenfüllend (Hausdorff-Dimension = 2).
Die Folgen können sehr einfach durch Falten eines Papierstreifens hergestellt werden (Wikipedia). Dieser wird mehrmals zur Hälfte nach rechts gefaltet. Anschließend klappt man das Band auf und formt die Knicke zu rechten Winkeln.
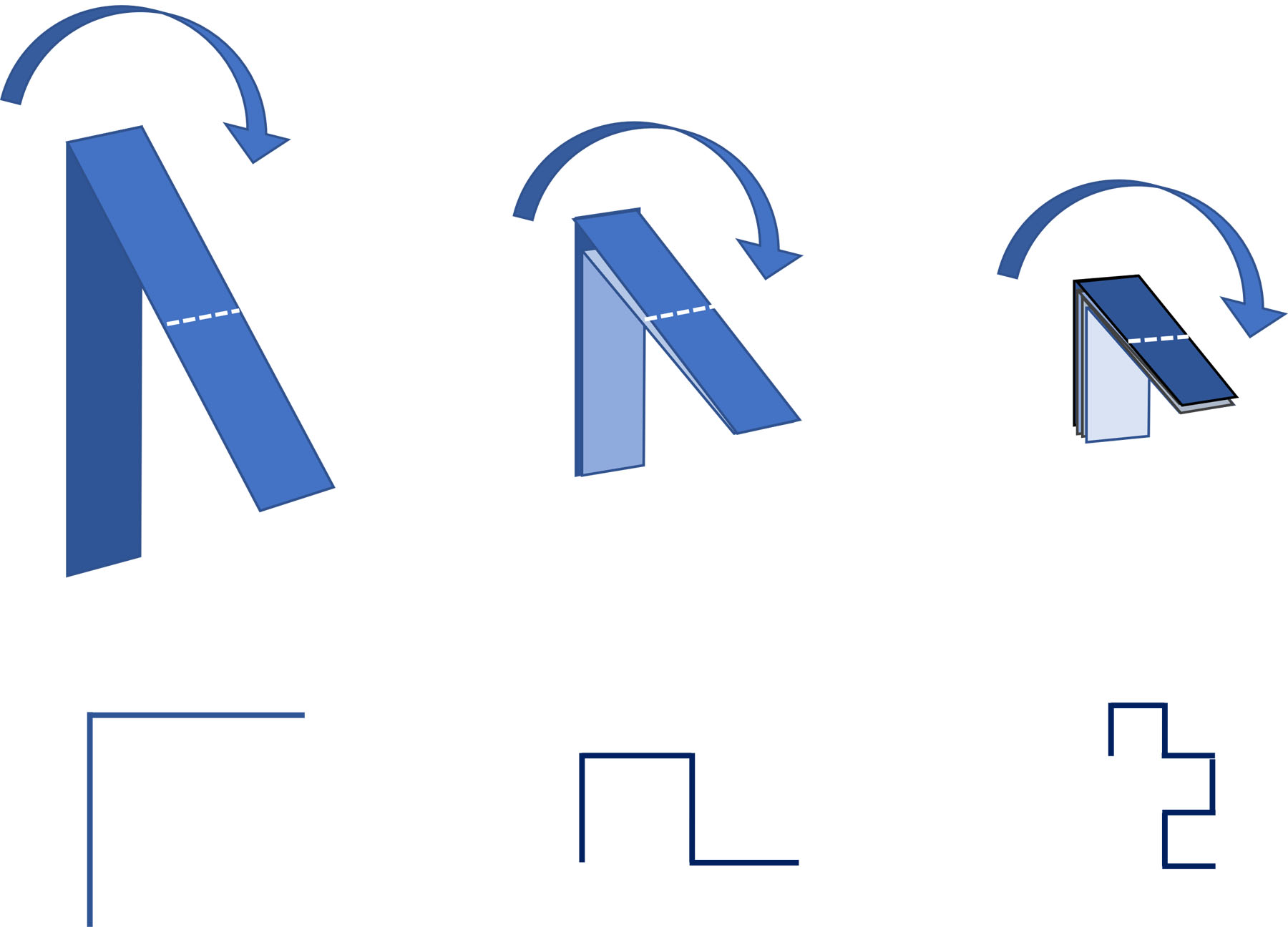
- Prusinkiewicz, P. and Lindenmayer, A. (1990) The Algorithmic Beauty of Plants. Springer, New York.
- Benoit B. Mandelbrot The Fractal Geometry of Nature , Freeman, San Francisco, 1982
- Harbich, T. (2021), On the Size Sequence of Diatoms in Clonal Chains in Diatom Morphogenesis (Diatoms: Biology and Applications) Vadim V. Annenkov (Editor), Richard Gordon (Editor), Joseph Seckbach (Editor), Wiley-Scrivener; 1. Edition
- USSING, A.P., GORDON, R., ECTOR, L., BUCZKO´ , K., DESNITSKIY, A.G. & VANLANDINGHAM, S.L. (2005). The colonial diatom ‘‘Bacillaria paradoxa’’: chaotic gliding motility, Lindemeyer Model of colonial morphogenesis, and bibliography, with translation of O.F. Müller (1783), “About a peculiar being in the beach-water”. Diatom Monographs, Vol. 5. Koeltz, Koenigstein, Germany.